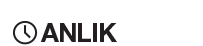İfadesi ve anlaması kolay olsa da teorem sanki biraz gariplik içeriyor görünmekte. Teoremin ifadesini birazdan vereceğiz ama kısaca öncelikle neden bir gariplik olduğunu açıklamaya çalışayım. Teorem kabaca verilmiş bir bölgenin alanla nokta saymak arasında bir ilişki veriyor. Diyebilirsiniz ki ne var bunda. Fakat bildiğiniz gibi alan dediğimiz şey çoğunlukla kenar uzunlukları, köşe açıları gibi kavramlara bağlıdır. Ama bu teoremde sanki bunları hepsini bir kenara bırakıp sadece nokta saymaya odaklanıyoruz gibi görünüyor.

Ama merak etmeyin durum o kadar da vahim değil. Başlangıçta garip görünen bu durum zamanla açıklığa kavuşacak. Şimdi bu kısa açıklamadan sonra teoremimizin ifadesini vermek için biraz hazırlık yapalım. İlk olarak çokgenin tanımıyla başlayalım.

Çokgen, düzlemde (iyi ayrıtı da sonsuza kadar uzatılmış düz bir masa yüzeyini düşünebilirsiniz) herhangi üç tanesi aynı doğru üzerinde bulunmayan belirli sayıda noktayı (konuşulan konunun anlamlı olabilmesi için nokta sayısını 3’ten büyük kabul edelim) ikişer ikişer birleştiren doğru parçalarının oluşturduğu kapalı şekillerdir.

Bu örneklerden ilk üç tanesine basit çokgen denir. Bunun nedeni bu çokgenlerin kendilerini kesmemeleridir. Son sıradaki çokgen ise basit olmayan bir çokgendir.

Şimdi düzlemde (iki boyutlu uzayda) uç noktalarının (köşe olarak isimlendirilebilir) koordinatları tamsayılar olan basit çokgenleri düşünelim. Aşağıda verilen basit çokgenler buna örnektir.

Düzlemdeki noktaların her birinin koordinatları \( (-1,1/2), ( \sqrt{2}, \sqrt{3} -1 ) \)  olabilir. Ancak birazdan ifade edeceğimiz teorem için biz sadece düzlemin koordinatları tamsayı olan noktalarıyla ilgilenelim (koordinatları tamsayı olan noktaların oluşturduğu düzlemin alt kümesi olan geometrik nesneye kafes denir).

Şimdi teoremimizi ifade etmek için her şeyimiz hazır gibi. İfade edeceğimiz teorem köşeleri kafes üzerinde olan basit bir çokgenin (kafes çokgen diyelim) sınırladığı alanın pratik olarak nasıl hesaplanacağıyla ilgili. Yani Şekil 2’de verilen mavi, sarı, yeşil alanların nasıl hesaplanacağıyla ilgili.

Bu teorem matematikte Pick Teoremi olarak adlandırılır. Teorem ilk defa 1899 yılında Avusturyalı matematikçi Georg Alexander Pick tarafından ifade edildi. Bu teoreme göre basit çokgenler tarafından sınırlanan bölgenin alanını bulmak için tek yapmanız gereken çokgenin sınırladığı alan içinde kalan kafes noktaları ve çokgenin sınırladığı alanın üzerindeki kafes noktaları saymak. Teorem formel olarak şöyle ifade edilir.

Pick Teoremi: \( P \) düzlemde verilmiş basit bir çokgen olsun. Bu çokgenin sınırladığı alan \( A \) olmak üzere, \( A \) bölgesinin alanı

             \( \mathrm{Alan}(P)  = i + \frac{b}{2} -1 \)

olarak verilir. Burada \( i \), \( A \) bölgesinin içerisinde kalan kafes noktalarının sayısı, \( b \) ise \( A \) bölgesinin üzerinde (sınırında) bulunan kafes noktalarının sayısıdır.

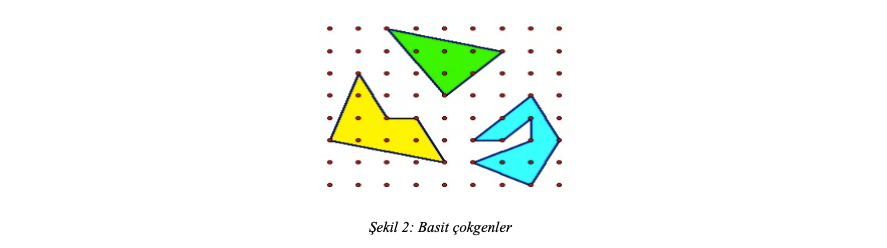
Hemen bir örnekle teoremimizin ne demek istediğini anlamaya çalışalım. Şekil 3’te mavi olarak belirtilen alanı hesaplamak istiyoruz diyelim.

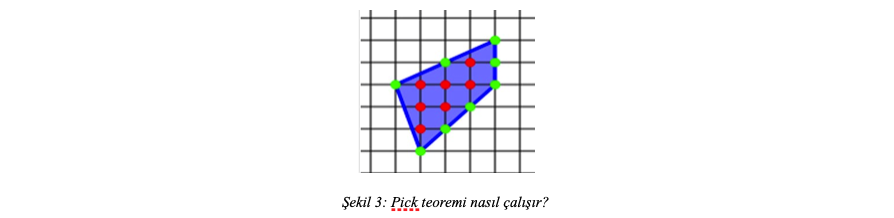
Bu örnekte \( i=7 \) ( bölgenin içindeki kafes noktalarının sayısı yani kırmızı noktaların sayısı), \( b=8 \) ( bölgenin sınırları üzerindeki kafes noktalarının sayısı yani yeşil noktaların sayısı) dir. Pick teoremine göre verilen çokgen tarafından sınırlanan mavi bölgenin alanı \( 7 + \frac{8}{2} -1 = 10 \) olarak hesaplanır.

Şimdi “kabaca” Pick Teoremi’nin neden doğru olduğunu göstermeye çalışalım. Bunun için öncelikle alanla ilgili basit bir gerçeği hatırlatalım. İki bölgeyi ortak kenarlarında birleştirerek oluşturduğumuz yeni bölgenin alanı bu iki bölgenin alanlarının toplamına eşittir. Şimdi bu durumun Pick Teoremi için de doğru olduğunu gösterelim. Yani iki çokgeni ortak kenarları üzerinden birleştirelim ve ortaya çıkan alanın bir toplama olup olmadığına bakalım.

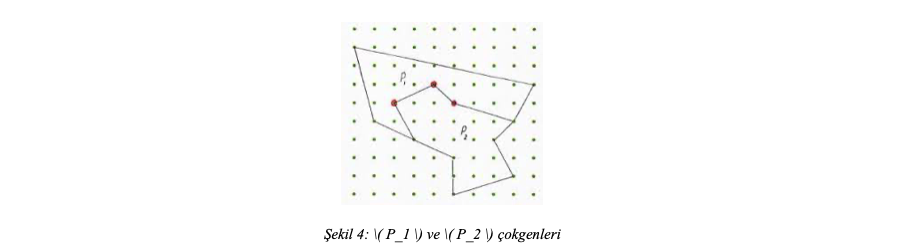
Şimdi \( P_1 \) ve \( P_2 \) çokgenlerinin birleştirilmesiyle oluşan yeni çokgeni, \( P \), düşünelim. \( i_1 \) ve \( b_1 \),  \( P_1 \) çokgeninin sınırladığı bölgedeki kafes noktalarının sayılarını, \( i_2 \) ve \( b_2 \), \( P_2 \) çokgeninin sınırladığı bölgedeki kafes noktalarının sayılarını göstersin.

Yeni bölgenin içindeki kafes noktalarının sayısı \( P_1 \) ve \( P_2 \)’nin içindeki kafes noktalarını kapsamakla birlikte Şekil 4 örneğinde kırmızı ile işaretlenmiş iç kafes noktalarını da kapsar.  Unutmayalım, Şekil 4’te verilen çizim sadece bir örnektir. Bu uyarıyı şu nedenle yaptık; normalde yeni bölgenin içerisindeki kafes noktalarının sayılarını bulurken ortak sınır üzerindeki noktaların sayısını bulmak kolay bir iş olmayacaktır. Aslında bu sayının o kadar da önemli olmadığını göreceğiz birazdan. Matematikte kullanılan çok yaygın bir metodu kullanacağız; bilmediğimiz ifadeye bir isim vereceğiz. \( P_1 \)  ve \( P_2 \) çokgenlerin ortak noktalarında bulunan kafes noktalarının sayısını \( x \) ile gösterelim.  Bu durumda \( P \)’nin iç kafes noktalarının sayısı \( i_P = i_1 + i_2 + x \) olur.

Peki yeni oluşan, \( P \)’nin sınırlarında bulunan kafes noktalarının sayısı nedir? Bu sayısı bulabilmek için \( x \) sayısını \( b_1 \) ve \( b_2 \) den çıkarmamız gerekir. Yalnız burada atlamamız gereken nokta kesişen kenarların uç noktalarını 2 defa saymış olmamız. Bu durumda \( P \)’nin sınırı üzerindeki kafes noktalarının sayısı ise \( b_P = b_1 – x + b_2 – x –2 = b_1 + b_2 – 2x -2 \) olur.

Şimdi \( P \) tarafından sınırlanan alanı bulmak için hazırız. Pick teoremini kullanırsak alanı aşağıdaki gibi hesaplarız.

\( i_P + \frac{b_P}{2} -1 = i_1 + i_2 + x + \frac{b_1 +b_2 – 2x –2 }{2} -1 = i_1 + i_2 + \frac{b_1 + b_2}{2} -1 \)

Yani eğer Pick Teoremi \( P_1 \) ve \( P_2 \) için doğruysa \( P_1 \) ve \( P_2 \)’nin birleştirilmesiyle oluşan yeni bölge \( P \) için de doğrudur. Yani Pick Teoremi toplama özelliğine sahiptir ya da toplama altında korunur diyebiliriz.

Yukarıda ispatladığımız önermeye toplama kuralı diyelim. Toplama kuralı biliniyorsa bu durumda Pick Teoremi’nin ispatı sadece matematiksel tümevarım yöntemiyle gösterilebilir. Ancak yazıyı daha fazla uzatmamak adına ispatın geri kalanını ifade etmekle yetineceğiz.

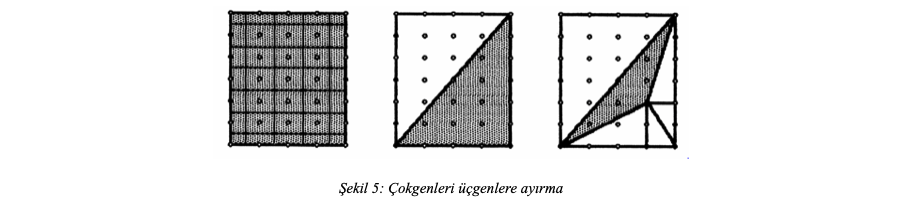
Şimdi diyelim ki elimizde karmaşık basit bir çokgen var. Bu çokgeni üçgenlere böleriz ve teoremi bu üçgenler için ispatlamaya çalışırız. Eğer üçgenler için doğruysa toplama özelliğinden bütün şekil için doğru olduğu gösterilebilir. Ancak üçgenler için ispat etmek için de bazı adımları izlemek gerekecek:

• Öncelikle teoremin birim kare için doğruluğu gösterilecek.
• Sonrasında kenarları eksenlere paralel olan dikdörtgen için teoremin doğruluğu gösterilecek.
• Dikdörtgen için doğruysa dikdörtgeni köşegen boyunca bölerek oluşturacağımız dik üçgen için de göstermek gerekecek.
• Son adım olarak ise, herhangi bir üçgen, dik üçgenler yapıştırılarak dikdörtgene tamamlanacak.

Bu adımları şekillerle göstermek istersek:

Merak edenler referanslar kısmında verilen kaynaklara bakabilirler. Özellikle Dale E. Varberg’in 1985 yılında verdiği ispatın çok zarif olduğunu belirtmek gerekir. Ayrıca Varberg’in makalesinde Pick Teoremi’nin genelleştirilmiş halini de bulmak mümkün.

[BAA - Matematik / Engin Özkan]

Kaynaklar:

• https://en.wikipedia.org/wiki/Pick%27s_theorem
• Pick’s Theorem Revisited, Dale Varberg, The American Mathematical Monthly Vol. 92, No. 8 (Oct., 1985), pp. 584-587
• Garip Eğriler, Tavşanları Saymak ve Diğer Matematiksel Keşifler, Keith Ball, Tübitak Yayınları, Çev: Boğaç Karçıka, 2017, Ankara